| Semesteroppgave matematikk: Poker og sannsynlighetsregning. |
Innhold:
Forord |
| Torgeir Frøystein B96
d Høgskolen i Oslo Allmennlærerutdanningen 1998 |
Spill fascinerer oss mennesker. Pensjonister blakker seg på kjøpesentrenes spilleautomater, familiefedre spiller seg fra hus og hjem og enkelte er i stand til å skape seg et levebrød av spill. For de aller fleste begrenser spill seg til en fast Lottokupong og et og annet flakslodd.
For min egen del har jeg etter hvert prøvd å tilnærme meg til spill på en litt forsiktigere måte og gjort en del for å få oddsen på min side. Jeg har vært med i tippelag som har maksimert innsatsen og tippet kompliserte systemer. (Med "hell" faktisk.) Jeg har vært på Bjerke travbane og tapt og vunnet, mest tapt, og sett at mangel på kunnskap skaper tapere.
I denne oppgaven kunne jeg godt ha sett på gambling og pengespill generelt. Det kunne f.eks. vært interessant å sett på hvor dårlig butikk det er å putte pengene sine på de spilleautomatene som befinner seg nesten overalt for tiden.
Når jeg nå har endt opp med poker er det fordi dette er det pengespillet jeg har det lengste forholdet til. Debuten kom i fjortenårsalderen med femøringer og har utviklet seg siden. Aldri lenger enn til småspill blant kamerater og kolleger, men like fullt en fascinasjon som kommer til å stå seg en stund. Poker er også et av de få pengespill hvor 100% av innsatsen går tilbake til spillerne.
Dette er en kortversjon av denne semesteroppgaven hvor jeg har luket bort de didaktiske problemstillingen av hensyn til det "brede publikum". Jeg vil etterhvert legge ut den fulle versjonen, men det blir i Word 6.0 format, og den vil da ligge her
Fra Tangdynastiet til Las Vegas.
Kortstokken har sin opprinnelse i Kina selv om det da ikke var i den for vi kjenner den i dag. En viktig faktor for utbredelsen av spillkort til erstatning for illustrerte trebrikker er trykkekunsten og papiret. Disse spillkortene hadde en annen for m enn den vi kjenner i dag, de var mer lange papirremser enn kort og illustrasjonene var helt andre.
Herfra vandret de langs karavaneveiene og fikk sin form, omtrent slik vi kjenner den, på denne ruten. Antageligvis i Tabriz, langs silkeveien.
I Europa dukket de opp rundt 1370. Her var også den store utbredelsen avhengig av trykkekunsten og fikk med denne en stor utbredelse.
Selve jokeren ble oppfunnet i 1857 og fikk sitt utseende etter navnet og ikke omvendt.
Poker har sin opprinnelse i et spill kalt primero som hadde en viss utbredelse i England og Spania på 16-1700 tallet, dette spillet er faktisk i bruk i Shakespeares skuespill: "Henrik VII". Fra dette utviklet seg spillet brag (England) og pocher (Tyskland, pochen "å banke") Allerede på dette tidspunktet gjenspeiler navnet spillets muligheter for å bløffe. Men det er franske kolonister som eksporterer spillet til USA hvor det sprer seg fra New Orleans, oppover Missisippi og videre vestover.
Rundt 1834 blir det endelig spilt med den kortstokken vi kjenner i dag, 52 kort, og spillet har fått sin endelige form. Det fikk raskt en stor utbredelse og i dag forbinder vi dette spillet med erobringen av vesten like mye som cowboys, nybyggere, seksløpere og prærievogner.
Pokeren fant veien tilbake til Europa rundt 1870 og en mann ved navn Robert Schenck skrev et sett med regler til spillet. Her besto korthendene av: Fire like, fullt hus, tre like, to par, et par og ingen par. Straight og flush kom altså til senere sammen med flere runder med satsing. Det er derfor en anakronisme når westernfilmer som beskriver poker fra før 1870 har med flere budrunder, straight og flush.
Spillet har siden gått sin seiersgang over hele verden og er verdens mest spilte kortspill. Kombinasjonen av penger, bløff, psykologisk kunnskap, og den så overvurderte mannlige egenskapen, pokerfjes, har nok gjort sitt til populariteten.
Poker blir av mange, bl.a. Sveriges kortguru Dan Glimne, regnet som det mest krevende av alle kortspill. Han hevder å sitere noen av verdens beste bridgespillere i denne påstanden. Det er kanskje derfor at det har oppnådd en slik enorm popularitet. "A minute to learn, a lifetime to master" er en gammel klisjé, men det finnes vel ingen områder hvor det er mer dekkende.
Poker er i utgangspunktet et meget enkelt spill. Hver spiller får utdelt fem kort og disse er rangert etter hvor store muligheter de forskjellige hendene gir. Etter som hvilken variant en spiller kan en forbedre de inngitte kort ved hjelp av kjøp eller lignende. Etter forskjellige regler etter hvilken variant en spiller, setter en penger på sine egne kort og den som har den høyeste hånden vinner.
Fordi det er penger med i bildet vil det ikke bli så enkelt. En spiller kan for eksempel sette så mye på sine kort at de andre gir seg. Det er også mulig at han faktisk ikke har kort av noen verdi. Til tross for det kan han likevel vinne potten. Det finnes utallige varianter av regler og budprosedyrer og halve spillet dreier seg i realiteten om penger og satsing. Mange av reglene for budgivning er i mange tilfeller kommet til for å gi mulighet for å øke potten.
Poker dreier seg derfor om mer enn ren matematikk, en må ha en viss kunnskap om mennesker, psykologi og kroppsspråk.
Vi skal nå se på de vanligste variantene av poker.
Dette er den varianten som er mest vanlig i USA. Runden begynner med at hver spiller får to kort. Et skjult og et synlig for de andre spillerne. Spillerne satser på disse to kortene og for hver gang de får et nytt kort. En får bare fem kort og det er derfor ikke noen mulighet for å forbedre den inngitte hånden. Dette handler selvfølgelig mye om bløff og psykologi og passer best for gambleren. Som regel vil en spiller med et par i bordet stikke av med potten.
Denne er også ganske populær i USA, men ikke like vanlig som 5-kort stud. Runden begynner som vanlig stud poker, men etter det femte kortet får spillerne to kort skjult. Dette gir mange muligheter for å sette sammen en pokerhånd. Dette spillet kjennetegnes av at spillet fort blir høyt og potten stor. Likevel vil en hånd med to høye par ofte stikke av med potten.
Denne er ikke spesielt kjent her hjemme, men er den varianten som spilles under VM i poker på Binion´s Horseshoe i Las Vegas. Spillerne får to skjulte kort og første budrunde går. Deretter legger giver tre kort åpne på bordet, disse er felles for alle spillerne. Det bys nå på nytt. Det deles ut to åpne kort til og det er ny budrunde for hvert av dem. I dette spillet kan det være med veldig mange spillere og det kan være fort gjort å klamre seg til potten for lenge. For å si som Kenny Rogers:
"You got'a know when to hold them,
know when to fold them,
know when to walk away,
know when to play."
Denne kjenner de aller fleste av oss fra hjemlige pokerlag. Hver spiller får tildelt fem kort og de inngitte hendene kan forbedres gjennom kjøp. Hvis en spiller forsiktig er dette sannsynligvis den "billigste" varianten av poker. Mesteparten av budene her vil foregå etter at den endelige hånden er kjent og med en viss erfaring vil en raskt vite om det vil lønne seg å spille videre på den inngitte hånden, eller om en skal kaste seg uten å delta i de avsluttende budrundene.
Jeg har valgt å legge vekten på denne varianten av to årsaker:
Jeg vil her først gå gjennom hvilke muligheter en har for de forskjellige hendene og til slutt presentere en oversikt med sannsynlighet for hver av dem.
Forskjellige hender i poker
Det er 52 kort i stokken og vi får utdelt 5 vilkårlige kort. Et kort kan ikke brukes flere ganger, dette gir 2.598.960 forskjellige kombinasjoner av fem kort.
![]()
Straight Flush
Straight Flush er fem kort etter hverandre i samme farge. I en farge er det
10 muligheter for det laveste kortet siden esset teller både en og fjorten.
Dette gir ![]() muligheter.
muligheter.
En del teller Royal Flush, ti, knekt, dame, konge, ess i en farge, som egen hånd, men jeg har regnet den inn som en Straight Flush.
Fire like
For fire like får vi tretten mulige verdier og det er bare en mulig hånd for
hver verdi, mens det siste kortet kan være hvilket som helst av de resterende
48. Dette gir ![]() muligheter.
muligheter.
Fullt hus
Hus består av tre like kort og et par. Da har vi:
Dette gir ![]() muligheter.
muligheter.
Flush
Fem kort i samme farge. Fem vilkårlige kort i en farge blir,tretten på fem. Vi må trekke fra de ti Straight Flushene og vi har fire farger. Dette gir
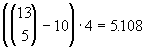 muligheter.
muligheter.
Straight
Fem kort i rekkefølge. Vi har igjen ti mulige verdier for laveste kort, og
hver av de fem kortene kan ha fire forskjellige farger. Til slutt må vi trekke
fra de førti Straight Flushene. Dette gir ![]() muligheter.
muligheter.
Tre like
Tre kort med lik verdi. Dette gir:
Da får vi:
![]() muligheter.
muligheter.
To Par
To forskjellige par gir:
Dette gir:
![]() muligheter.
muligheter.
Et Par
Et par gir:
Dette gir: ![]() muligheter.
muligheter.
| Hånd | Muligheter | Muligheter/ Antall hender* |
Odds, sannsynlighet |
| Straight Flush | 40 |
40 : a = |
O,0000154 |
| Fire like | 624 |
624 : a = |
0,00024 |
| Hus | 3 744 |
3 744 : a = |
0,00144 |
| Flush | 5 108 |
5 108 : a = |
0,00197 |
| Straight | 10 200 |
10 200 : a = |
0,00392 |
| Tre like | 54 912 |
54 912 : a = |
0,0211 |
| To par | 123 552 |
123 552 : a = |
0,0475 |
| Par | 1 098 240 |
1 098 240 : a = |
0,422 |
| Hender med verdi | 1 296 420 |
1 296 420 : a = |
0,499 |
Antall hender 2 598 960=a
Som vi ser er sannsynligheten for å få inngitt en hånd av verdi tilnærmet lik en halv. Dette gir oss med andre ord en starthånd av verdi cirka annen hver gang. Med dette utgangspunktet kan det være greit å ha en viss oversikt over hva som skal til for å øke denne verdien.
Dette er for mange den mest spennende delen av spillet, en har bestemt seg for å satse og har valgt hvor mange kort. Nå gjelder det, har en fått det en absolutt håper på, eller i hvert fall en forbedring.
Jeg vil her ta for meg de vanligste starthendene og se hvilke sannsynligheter en har for å forbedre de enkelte. Felles for alle er at siden du allerede har fått fem av kortene er det 47 kort å ta av.
Som vi etter hvert vil se er det ikke så gode sjanser for å forbedre en korthånd ved kjøp og at odds høyere enn 0,1 er å regne som bra.
Et par
Her vil det være av interesse hvor mange mulige kombinasjoner det finnes ved kjøp av tre kort av et utvalg på 47. Det gir:
![]() mulige kombinasjoner
mulige kombinasjoner
Kjøp på et par kan gi:
To par: Vi må kjøpe et par, hvor mange par finnes det å
kjøpe, vi har:
Dette gir: ![]() mulige par som
gir oss en sjanse på
mulige par som
gir oss en sjanse på
3168 : 16.215 = 0,195
Tre og fire like: Det er to kort som kan gi oss tre like og vi greier oss med et av dem, vi har tre sjanser til å trekke dette kortet, skal vi ha fire like må vi ha begge kortene. Vi bruker hypergeometriske sannsynligheter, og har et utvalg på tre, en populasjon på 47 og to spesielle utfall. Vi får:
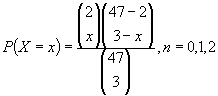
Og det gir oss følgende verdier for P (X=x)
| P (X= 0) | P (X=
1), Tre like |
P
(X=2), Fire like |
0,875 |
0,122 |
0,00278 |
Altså en sannsynlighet på 0,122 for tre like og 0,00278 for fire like. Det er nok ikke så rart at fire like forekommer uhyre sjelden, jeg kan telle på en hånd de gangene det har skjedd meg.
Fullt hus: Denne blir litt vrang, du kan enten få et kort til av de du allerede har + to av en annen verdi, eller tre like av en annen verdi. Vi regner hver for seg og legger sammen,
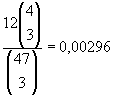
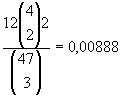
Dette gir summen: 0,01184 som er sannsynligheten for å kjøpe seg til fullt hus fra to par.
Fire like: Det er to kort som kan gi fire like og vi må ha begge. Altså to spesielle, 47 mulige og tre sjanser.
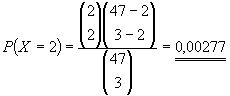
To par
Et kjøp på to par kan gi Fullt hus. Det er fire kort
som kan gi deg fullt hus, det gir: 4 : 47 = 0,085,
Ikke så stor sjanse med andre ord, men to par er i seg selv en
god hånd.
Her kan en jo vurdere en bløff og ikke kjøpe noe, det vil skremme noen til å tro at du sitter med en full hånd. Spesielt siden en som sitter med et par har bedre odds for å kjøpe seg en hånd som slår dine to par enn du har til å forbedre din hånd. (Se kjøp på et par, tre like.)
Tre like
Kjøp på tre like kan gi:
Fire like: Et gunstig kort, du har to sjanser, det gir:

Fullt hus: Da mangler vi et par, det har vi gjort før:
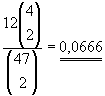
Tre i samme farge
Kan gi både et og to par, men vi konsentrerer oss om:
Flush: vi har ti spesielle og skal trekke to, det gir:

Kjøp av et kort
Når vi nå skal kjøpe bare et kort, vil sannsynlighetsregningen begrense seg til å telle antall mulige og antall gunstige. Det kan jo virke litt banalt, men jeg syntes jeg måtte ha med alle kombinasjonene. Det er også litt viktig å vise hvor dårlige odds det gir til tross for at mange ser ut til å tro det motsatte.
Fire i samme farge
Kjøp på fire i samme farge kan gi:
Et par: Det er tre kort i fire verdier som kan gi et par, d.v.s. tolv gunstige, vi får:
12 : 47 = 0,255
Flush: Det er 9 kort som kan gi flush, 9 : 47 = 0,19 hvilket ikke er så verst
Straight drag, fire kort, ett kort mangler
Det er et kort som mangler på en Straight, det er fire kort som oppfyller kravet, det gir 4 : 47 = 0,085 som er særdeles dårlige odds.
Straight drag, fire kort, åpen i begge ender
Her mangler det også et kort, men det er åtte kort som
oppfyller kravet, det gir
8 : 47 = 0,17 som er bedre. En god regel er med andre ord
å ikke kjøpe for en straight med mindre det er to verdier som
gir deg det ønskede resultatet.
Fire kort, samme farge, i rekkefølge, åpen i begge ender.
Dette regnes som en kanonhånd, sjansen for flush er 0,19, sjansen for straight er 0,17, (se over)altså en sjanse på 0,19 + 0,17 = 0,36 for flush eller straight som begge regnes som "vinnerhender" mens du har en sjangse på 2 : 47 = 0,043 for en straight flush, som er en vinnerhånd. Selvfølgelig er sjansen for å få en slik hånd inngitt veldig liten, men det skjer jo av og til.
I poker kjøper spillerne kort etter tur. Hvordan en skal tolke de andres kjøp blir ofte et spørsmål om hvor mange som sitter før og etter deg. Et kjøp kan tolkes som en melding om hvor gode kort en har. Sitter du tidlig i runden må du ha gode kort for å kjøpe siden ingen av de andre har meldt sin interesse og du ikke vet hva de kan sitte med, mens sitter du helt til slutt og de andre har meldt "jekk" (d.v.s. at de kaster seg hvis ikke alle vil være med å spille om en ny giv med kort) kan du kjøpe på relativt lave kort.
Samtidig vil antall kjøpte kort hos motspillerne gi en indikasjon på hva de kjøper på. Det er egentlig denne runden som skiller de gode spillerne fra de dårlige, ikke så mye på hvordan de kjøper kort, men på hvordan de følger med på og tolker de andre spillernes kjøp. Samtidig vil mange avsløre gjennom kroppsspråk og annet hva de har, ikke har å fare med.
En hånd som mangler et kort på å bli full, regnes av mange som sterk, men det viser seg at oddsen for å få den fulle hånden er minimal. Så om noen kjøper et kort så kan du faktisk regne det som to par og spille deretter. Dette er litt i motsetning til hvordan de fleste erfaringsmessig spiller, kjøper du et kort blir du regnet som farlig selv med så dårlige odds på din side.
Etter hvert som en har fått et bilde av hvordan motstanderne spiller, og hvordan de avslører seg, er det aspektet med å bløffe seg til en pott som legger enda en dimensjon til spillet. Tor Edvin Dahl beskriver pokerspillet som et bilde av den amerikanske drømmen, på den måten at det er likegyldig hvordan du spiller spillet, så lenge du er en vinner. Hvis man gjennom bløff og godt spill kan vinne så høster man anerkjennelse, mens blir du avslørt, høster du bare medynk.
Å sitte i bakhånd er selvfølgelig en fordel, siden da har allerede de andre avslørt mye av sitt spill, men også i forhånd kan du gjøre mye hvis du greier å gi de andre et bilde av spillet ditt som avviker fra det du virkelig har.
Bløffe kan du selvfølgelig gjøre begge veier. Du kan få de andre til å tro du har bedre kort enn du har, men også lure dem andre veien for å få dem til å tro du er et lett bytte.
Alspach's Mathematics and Poker Page
Dette er sidene til en professor i matematikk som har en stor
interesse for poker. Her kan du lære mye om poker og
sannsynlighetsregning.